恐らく、この記事を読んで下さっている方は「地絡計算」で困っている人ではないだろうか??
今日はここを解説しておく。
おはようございます。
電験と電気業界を研究している桜庭裕介です。
初めての方もいらっしゃると思いますので、いつもの簡単な自己紹介を添えておきます。
≪実績≫
❑転職関係❑『残業10時間以下』&『年収変動なし』の企業に転職成功
※詳細を下記のnoteに集約
電気エンジニアとしての決断【超大手企業を退社する選択】
❑電験研究歴❏
✔トータル100年分の過去問を分析
・電験1種 40年分
・電験2種 40年分
・電験3種 20年分
✔雑誌連載を開始
「理論の超入門」
❑TOEIC❑✔半年で885点取得
一言で言うと、電験をずっと分析してきた人間。
夢はある?と最近聞かれた。
電気、プラントの運転操作を教えて、自分が飯を食えれば最高だと答えた。
妻子なしなら、小さなアパートの一室で納豆や卵とごはんだけの食事で暮らすと思う(栄養の事は無知)
今後、確実に介護施設の問題が挙がる。
そこに貢献できれば良い。
そんな事を考えている。
静電容量Cについて
通常、理論科目で出てくるときに静電容量で困ることはあまりない。型が決まっていて、分流するにしろ、分圧するにしろ、合成抵抗を求めるにしろだ。
だが、電力科目になって、知識不足というか、別の視点からの問があることで困ることがある。※
それが「静電容量のΔ-Y変換」である。
具体的には「地絡計算」で出てくる。
※単に理論科目で静電容量のΔ-Y変換が出ないだけである
静電容量のΔ-Y変換を考える
まずはΔ-Y変換を「抵抗R」で考えてみよう。
(困った時は基本的に抵抗で考えるとスムーズにいくのでオススメだ)
全ての抵抗がRだとしたら
(R×R)/(R+R+R)=R/3
でY変換後の抵抗は求めることができる。
俗に「同じ抵抗をΔ-Y変換したら1/3になる」というものである。
ではここからが本題。
静電容量でΔ-Y変換をしてみよう。面白いものが見えてくる。
実際の計算
Δ-Y変換の公式に静電容量を入れてみよう。
「・・・!!!!」

「静電容量×3」になっている!!!
分母に来る3が、分母にいる静電容量にかかるのか!!!
結論
静電容量はインピーダンスに直したとき、抵抗とは違い、分母側に静電容量が入る。
つまり、実際にはインピーダンスとしては3分の1になっている。
この点は抵抗と変わりないのである。
問題集の解説の中には横着をし
ケーブルの静電容量のΔ-Y変換をするので、静電容量は3線分だから3C
とサラッと書いているものがある。
こういう所が分からんのだ!と憤慨したい気持ちになることがあるだろう。
そういった所で悩む人に届くことを願って、この記事を書いた。
電験の試験に向かって、共に頑張ろう!!
静電容量のΔ-Y変換に関する問題
リクエストがあったので、問題を紹介しておく。
この問題は教科書に記載されていることもある代表格だが、それ故に考え方が難しい。
(誰だよ、この知らないと困るような例題を問題として出題したバ〇は・・・おっと怒られるのでやめておく)
平成29年(2017年)問16
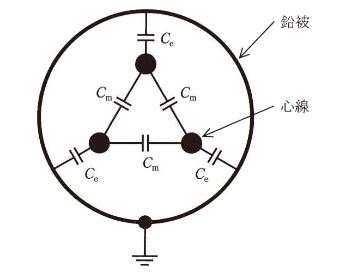
問題文
図に示すように、対地静電容量 Ce[F]、線間静電容量 Cm[F]からなる定格電圧 E[V]の三相1回線のケーブルがある。今、受電端を開放した状態で、送電端で三つの心線を一括してこれと大地間に定格電圧 E[V]の1/√3倍の交流電圧を加えて充電すると全充電電流は 90Aであった。次に、二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線と大地間に定格電圧 E[V]の 1/√3倍倍の交流電圧を送電端に加えて充電するとこの心線に流れる充電電流は 45Aであった。
次の(a)及び(b)の問に答えよ。ただし、ケーブルの鉛被は接地されているとする。また、各心線の抵抗とインダクタンスは無視するものとする。なお、定格電圧及び交流電圧の周波数は、一定の商用周波数とする。
(a) 対地静電容量 Ce[F]と線間静電容量 Cm[F]の比Ce/Cmとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.5 (2) 1.0 (3) 1.5 (4) 2.0 (5) 4.0
(b) このケーブルの受電端を全て開放して定格の三相電圧を送電端に加えたときに 1線に流れる充電電流の値 [A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 52.5 (2) 75 (3) 105 (4) 120 (5) 135
解説
この問題の解説は、問題自体話題になったこともあり、皆がこぞって解説しているから、既に解答は手元にあるだろう。
この問題でちゃんと押さえておかないといけないポイントは
①静電容量Cs(鉛被に繋がっている)が接地しているから電位0。つまりはY結線になるという点
②静電容量CmはΔ-Y変換でCsと並列回路になるという点
ここを理解するというハードルがあるので、お節介ながら記載しておいた。このように書いておくとめちゃくちゃ理解しやすいと思う。
解説と合わせて読んでもらえると良いだろう。特に①。
あとは3倍になる静電容量をにやにやしながら、処理していけば良いのである。
