電験3種の理論過去問をサッと引き出せるようにすることがこの記事の目標だ。
共に要点を押さえる学習をしていこう!!!
≪前回まで≫
平成29年問5
直流回路
≪問題≫
20Ωに流れる電流を求めなさい。
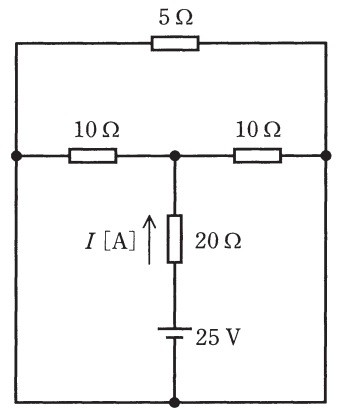
≪選択肢≫
(1)0.5 (2)0.8 (3)1.0 (4)1.2 (5)1.5
この問題はパッと見ると、Δ-Y変換をしたくなる。
だが、それでは手間もかかる上にミスをする可能性が出てくる。
こういう電気回路を見たときに頭に入れておいて欲しいのが
対称性
だ。
電磁気もそうだが、対称である場合、何らかのショートカットがある。
この直流回路の問題で言えば、対称であれば
電位が同じ
つまりは
電流が流れない
として考えることができる。
5Ωを取り払ってしまえば、怖いものは何もない。
20Ωと10Ωの並列回路との合成抵抗を求め、電圧を割ってやることで、電流を求めることができる。(10Ω同士の並列回路の合成抵抗は「5Ω」。20Ω+5Ωが全体抵抗になる)
答えは(3)だ。
■コメント■
6月5日分は簡単だったね!問題を見てΔ-Y変換だ!と一点に集中してしまうと、Δ-Y変換ですらミスをしてしまいがち。
まずは冷静にどう解こうかな?と考える余裕が身に付くまで頑張って問題を解こう。
速度については、計算をスラスラ解けるという部分さえ向上すればいい。冷静になれば解けないことはない問題も多いのだ。
参考
Δ-Y変換で躓いたという声があったので、メモ書きを共有しておきます。回路変形がややこしい。
苦手な人の共通点としては接続点移動だろう。
※汚いメモ書きで申し訳ない。


「2Ωが並列接続されているから移動できる」が理解できない人が多いが、25Vを含む真ん中の回路に並列接続という観点で考えると飲み込みやすいだろう。

平成29年問6
直流電源とコイル・コンデンサ
≪問題文≫
R1=20 Ωの抵抗、R2=30 Ω の抵抗、インダクタンス L1=20 mH 、L2=40 mH のコイル及び静電容量 C1=400 μF 、C2=600 μF のコンデンサからなる図のような直並列回路がある。直流電圧 E=100 V を加えたとき、定常状態において、L1、L2、C1 及び C2 に蓄えられるエネルギーの総和の値 [J] として、最も近いものを次の(1)~(5)のうちから一つ選べ。

≪選択肢≫
(1)0.12 (2)1.20 (3)1.32 (4)1.40 (5)1.52
理論科目の問6は王道の問題が多いので確実に解いていきたい。
この問題で重要になるのは
定常状態の意味
である。
定常状態におけるコイル、コンデンサはどんな素子になるのかを理解しているかが問われている問題だ。
まず、コンデンサの話をする。
定常状態のコンデンサは電荷の充電が完了してしまえば、電流を通さなくなってしまう。
問題で問われているエネルギーを算出する為には「電流」を求める必要がある。
つまり、何が言いたいかというと
電流を求める際は「コイルと抵抗」だけを考えればよい
ということだ。
しかも、定常状態のコイルは直流成分に対しては抵抗は0。短絡銅線と見なすことができるのだ。当然、コイルに発生する電圧も0だ。(コイルは直流電流が流れると瞬間的に電圧が発生する)
ここまで知識があれば、電源電圧100Vを合成抵抗50Ωで回路全体に流れる電流は2Aであることを求めることができるし、C1とC2にかかる電圧も分かる。
C1にかかる電圧はR1にかかる電圧、C2にかかる電圧はR2にかかる電圧と同じ。
あとはコイルとコンデンサのエネルギー算出の公式に当てはめてやればいい。
コイルのエネルギーを求める公式
1/2LI^2
コンデンサのエネルギーを求める公式
1/2CV^2
答えは(5)だ。
■コメント■
6月6日分のこの問題は「公式」と「知識」が必要だった。知らないと手も足も出ない・・となるので、絶対に基本を押さえておこう。過去問を解け!というアドバイスがあるが、こういうポイントを押さえる学習に意味がある。
平成29年問7
キルヒホッフの電流則
※7日22時に更新予定だ!(現在、2:28分)仕事が沢山溜まっているが・・・頑張っていくぜー!!!なかなか時間に間に合わず申し訳ないが、とにかく問題にぶつかって解消していくぞー!!!
申し訳ないです!
4時まで寝ます!!
仕事が終わらず、問い合わせにも答えてました。
いつも見てくれてありがとうー!!!
※キナリ杯という朝日新聞に載るほどのイベントに参加したら、思わぬ形で自分の文章を読みたいという人が増えた。挑戦ってやっぱり大事だ。勉強のやる気が出るようなことを書いているので、もし良かったら読んでみてくれー!!とはいえ、勉強の休憩時間に読むこと。それだけは約束してくれ!!!